Table of Contents
Some important Graph
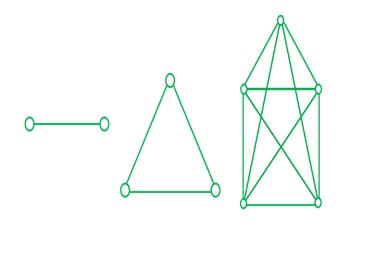
1-Complete Graph:A simple connected graph is said to be complete if each vertex is connected to every other vertex.
Example
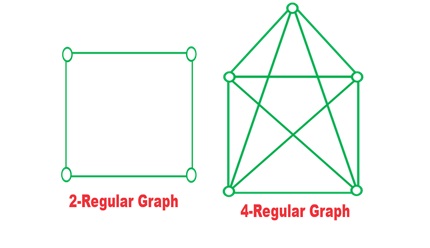
2-Regular Graph: A graph G is said to be regular if every vertex has the same degree if degree of each vertex of graph G is K , then it is called K-regular graph.
Example
3-Bigraph(or Bipartite): If the vertex set V of a graph G can be partitioned into two non-empty disjiont subsets X and Y in such a way that edge of a G has one end in X and one end in Y than G is called bipartite.

4-Connected Graph: An undirected graph is said to be connected if there is a path between everytwo vertices.
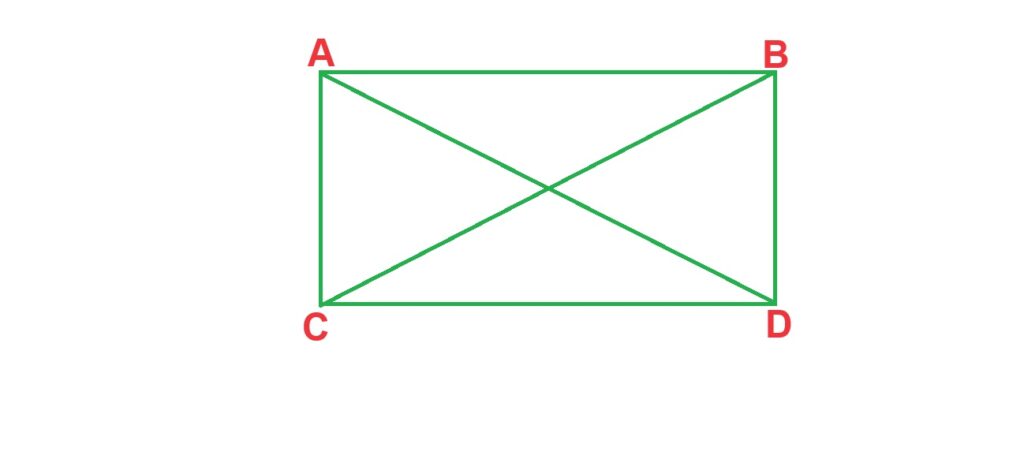
Note: If a graph is connected then it will not bipartite.
5-Complete Bipartite Graph: If every vertex in X is disjiont is every vertex in Y, then it is called a complete bipartite graph.
If X and Y condition m & n vertices then this graph is denoted by Kmn.

6-Subgraph: Let G(V,E) be a graph ,let V be a subset of V and let E be a subset of E whose end point belong to V Then G (V,E) is graph & called a subgraph of G(V,E)
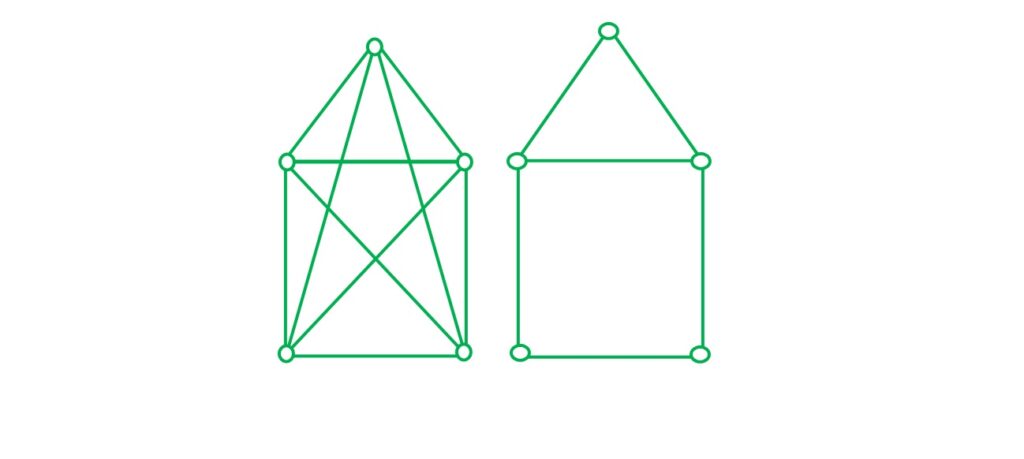
7-Decompostion of Graph: A graph is said to be decomposed into two subgraph G1 and G2
if G1 V G2 =G and G1 ^ G2= null graph.

8-Complement of Graph : Complement of a graph G is defined as a simple graph with the same vertex set as G and where two vertices U and V are adjacent only where they are not adjacent in G.
Example
9-Planare Graph: A graph which can be drawn in the plane so that its edges do not cross is called planase.